Kapitel 1 - Einführung in die Radioaktivität
1.1 Ursprünge radioaktiver Strahlung
1.2.2 Wirkung der Strahlung auf den menschlichen Körper
Kapitel 2 - Radioaktiver Zerfall
2.1 Einführung in das Bohrsche Atommodell
2.2 Verschiedene Strahlungs- und Zerfallsarten im Detail
Kapitel 4 - Mathematische Beziehungen
Kapitel 5 - Altersbestimmung mit der Radiokarbonmethode
5.2 Aufnahme in den Organismus
5.3 Zerfall von Kohlenstoff 14
5.4 Einschränkungen bei der Anwendung
Kapitel 6 - Die Uran-Blei Methode
Kapitel 7 - Anwendungen der Kohlenstoff-14 Methode und der Uran-Blei Methode
7.1 Aufgaben zur Kohlenstoff-14 Methode:
7.2 Aufgaben zur Uran-Blei Methode:
Anhang - Diese Ausarbeitung existiert auch als
Hendrik Bermpohl
Maximilian Drees
Sebastian Florczak
Dominik S. Herwald
Arno Klenke
Jan Möllers
Josef Pozny
Marius Schirmer
Simon Schwichtenberg
Philip Stoffel
Daniel Welp
Kurslehrer: Bernhard Freitag
Physik GK 13
Goerdeler Gymnasium
2004
Wie oft lesen wir in der Zeitung über archäologische Funde, die tausende von Jahren alt sein sollen? Doch wie wird ihr Alter ermittelt?
DJ Ötzi könnte man nach seinem Alter fragen - doch beim Ötzi aus den Ötztaler Alpen ist dies natürlich nicht möglich.
Die Radioaktivität gibt uns jedoch die Möglichkeit, eine Altersbestimmung durchzuführen. Dazu müssen wir jedoch zunächst einmal klären, was Radioaktivität überhaupt ist. Dies soll im Rahmen dieser Arbeit geschehen.
Radioaktive Strahlung gab es schon immer auf der Erde. Ein Teil dieser sog. terrestrischen Strahlung hat seinen Ursprung in Elementen, die schon immer auf der Erde vorhanden sind.
Es existieren also gewisse Elemente, wie z.B. das Uran, die radioaktive Strahlung aussenden. Dabei werden Teilchen des jeweiligen Atoms abgestrahlt und somit dessen Beschaffenheit verändert. So entsteht bei jedem Schritt dieses Kernumwandlungsprozesses ein anderes Element. Er setzt sich solange fort bis ein Element entstanden ist, welches nicht mehr zerfallen kann (ein stabiles Element wie z.B. Blei).
Ein anderer Teil der auf der Erde vorhandenen Strahlung wird durch die aus dem All kommende Strahlung gebildet. Es trifft ständig eine Teilchenstrahlung, die ihren Ursprung z.B. auf der Sonne oder anderen Sternen hat, auf unsere Atmosphäre auf. Diese Strahlung wird als kosmische Strahlung bezeichnet.
Ein Großteil dieser Strahlung wird jedoch vom Magnetfeld der Erde abgelenkt - wäre dies nicht der Fall hätte vermutlich niemals Leben auf der Erde entstehen können, da die Strahlung eine für Organismen schädliche Wirkung besitzt. (s. 1.2.2)
Es gibt grundlegend drei verschiedene Strahlungsarten. Die Alpha-, Beta- und Gamma-Strahlung:
Je nachdem welcher Dosis (Strahlenmenge) der radioaktiven Strahlung der menschliche Organismus ausgesetzt wird, kann dies fast gar keine bis hin zu einer tödlichen Wirkung besitzen. Die ständig auf der Erde vorhandene natürliche Strahlung hat beispielsweise kaum Folgen für den Menschen, da er sich im Laufe der Evolution daran anpassen konnte. Bei künstlich erzeugter Radioaktivität, wie in Atomreaktoren, ist dies natürlich nicht der Fall.
Die verschiedenen Strahlungsarten haben aufgrund ihrer Beschaffenheit unterschiedliche starke Wirkungen auf den menschlichen Körper:
Die Alpha-Strahlung besitzt die schädlichste Wirkung der Strahlungsarten. Beta- und Gamma-Strahlung haben in etwa gleich starke Auswirkungen. Bei Gamma-Strahlung besteht jedoch die Besonderheit, dass diese den menschlichen Körper vollständig durchdringen kann.
Als Maßeinheit für die Aktivität A radioaktiver Elemente wurde das Becquerel eingeführt. Es gibt die Anzahl (∆N) der Kernumwandlungen pro Zeiteinheit (∆t) an:
Größe:  |
Einheit:  |
Zum Nachweis radioaktiver Strahlung macht man sich die ionisierende Wirkung der Strahlung zunutze. D.h., wenn die Strahlung auf ein Atom trifft, werden Elektronen aus den Hüllen dieses Atoms herausgeschlagen. Dadurch ist das verbliebene Atom nicht mehr elektrisch neutral, sondern ein positiv geladenes Ion, welches leichter nachweisbar ist.
Es gibt mehrere Methoden zum Nachweis radioaktiver Strahlung. Hier soll beispielhaft nur das Geiger-Müller-Zählrohr beschrieben werden:
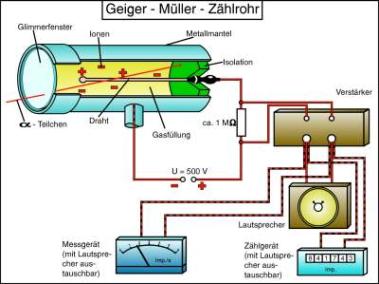
Das Geiger-Müller-Zählrohr besteht aus einem mit Gas gefüllten Metallrohr in dessen Mitte sich ein Draht befindet.
Zwischen Metallmantel und Draht wird eine hohe Spannung angelegt.
Die Strahlung kann durch ein Glimmerfenster in den Hohlraum gelangen. Durch die ionisierende Wirkung wird das Gas leitend. Es kann nun ein Strom zwischen Mantel und Draht fließen. Die Leitfähigkeit des Gases lässt jedoch schnell wieder nach, weswegen man jeweils nur einen kurzen Impuls (Stromstoß) messen kann.
Die Anzahl dieser Impulse pro Sekunde gibt die Aktivität wieder.
Um die Einzelheiten des radioaktiven Zerfalls zu verstehen, ist es notwendig, über den Aufbau von Atomen informiert zu sein. Ein hierzu ausreichendes Modell ist das Bohrsche Atommodell.
Elektronen auf äußeren Bahnen besitzen mehr Energie, als Elektronen auf inneren Bahnen, es gibt bei den Elektronen also verschiedene Energiestufen. Genauso existieren auch für die Protonen des Kerns verschiedene Energiestufen.
Die Notation 
bedeutet, dass das Kohlenstoff-Atom C im Kern eine positive Ladung von 6 Protonen enthält. Die Zahl 14 gibt die Anzahl aller Kernbauteile (Nukleonen) an (Protonen und Neutronen). Protonen und Neutronen haben etwa dieselbe Masse, nämlich 
. (1u ist dabei die sog. atomare Masseneinheit.) Das bedeutet, dass insgesamt 14 Nukleonen im Kern enthalten sind, also 8 Neutronen. Die Masse der Elektronen ist so gering, dass sie hier nicht relevant ist.
Bei Atomen mit besonders hoher Anzahl an Protonen, sind die Abstoßungskräfte im Kern auch besonders groß. Daher kann es passieren, dass 2 Protonen und 2 Neutronen, dies entspricht einem Helium-Kern, vom Kern abgespalten werden und als α-Strahlung emittiert werden.
Ein Beispiel ist der α-Zerfall von Thorium: 
.
Der β--Zerfall tritt besonders bei hoher Anzahl von Neutronen im Kern auf. Dann ist die Wechselwirkung zwischen Neutronen und Protonen schwächer, da diese auf die vielen Neutronen verteilt ist. Ein Neutron wird dann gespalten in ein Elektron und ein Proton. Der Kern emittiert das Elektron als β-- Strahlung.
Die Bilanzgleichung für den β--Zerfall lautet: 
.
Beim β+- Zerfall zerfällt ein Proton in ein Neutron und ein Positron. Ein Positron ist einem Elektron ähnlich, besitzt also eine vernachlässigbar geringe Masse, der Unterschied ist, dass Elektronen negativ geladen sind, Positronen positiv. Das Positron wird wieder als Strahlung emittiert.
Hier lautet die Bilanzgleichung: 
.
Wenn in Atomkernen die Anzahl der Protonen steigt, zum Beispiel durch β--Zerfall, steigt damit auch die positive Ladung des Kerns. Also wird auch die Anziehungskraft zwischen Elektronen und Protonen größer, so dass es passieren kann, dass Elektronen aus der innersten Bahn, der so genannten K-Schale, vom Kern "eingefangen" werden. Aus dem Elektron entsteht dann, zusammen mit einem Proton, ein Neutron. Da in der K-Schale nun ein Elektron weniger vorhanden ist, springt von einer äußeren Schale ein Elektron in die K-Schale. Da Elektronen in der K-Schale aber weniger Energie haben, als Elektronen in äußeren Schalen, wird diese Restenergie in Form von Röntgenstrahlung, einer speziellen Form der elektromagnetischen Strahlung, abgegeben.
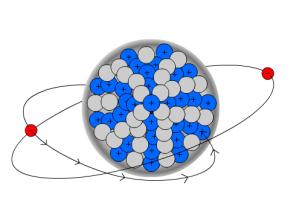
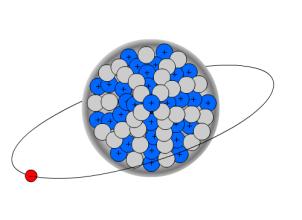
Die Bilanzgleichung zum K-Einfang sieht folgendermaßen aus: 
.
Wie schon oben erwähnt, kann auch der Kern verschiedene Energiezustände einnehmen. Die nach einem der oberen vier Zerfallsarten entstandenen Kerne befinden sich oft in einem anderen Energiezustand, als beim Standardzustand. Beim Übergang in diesen Standardzustand wird die überschüssige Energie in Form von elektromagnetischer Strahlung ausgesendet.
Die Nuklidkarte ist eine Tabelle, ähnlich dem Periodensystem der Elemente, auf der natürliche und künstliche Nuklide in einem System aufgeführt sind. Dabei werden in den Zeilen die verschiedenen Elemente aufgeführt, wobei die Zahl der Protonen nach oben hin zunimmt. In den Spalten sind die Isotope (Nuklide) dieser Elemente aufgeführt und Zahl der Neutronen nimmt nach rechts zu. Das bedeutet auch, dass die Masse nach rechts hin zunimmt. Am Anfang der Spalte steht das Element, mit dem Mittelwert der entsprechenden Isotope. Außerdem ist bei den Nukliden noch die Halbwertszeit angegeben.
Wenn man nun eine Zerfallsreihe bestimmen will sucht man zuerst das Startnuklid heraus. Nun sieht man anhand der Farben (die in der Legende erklärt sind) welche Zerfallsarten es bei diesem Nuklid gibt. Dann geht man anhand der jeweiligen Zerfallsart auf das nächste Nuklid. Dies macht man so lange bis man zu einem stabilen Nuklid kommt. Gibt es mehrere Zerfallsarten, bei einem Nuklid, so muss man mehrere Wege gehen.
Bei den verschiedenen Zerfällen kann man nach folgenden Regeln vorgehen:
Ein Beispiel für eine Zerfallsreihe ist der Zerfall von 232Th zu 208Pb.
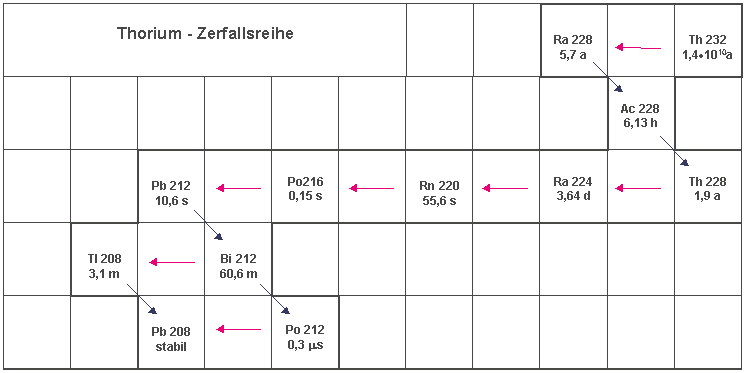
Es folgt nun ein Auszug aus einer Nuklidkarte, bei der als Beispiel der α-Zerfall von 228Th, welches zu 224Ra zerfällt, stärker umrandet ist.
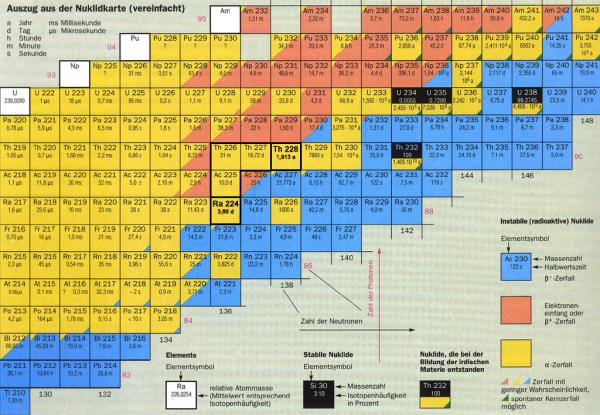
Wie man sicher schon vermuten kann, kommt man auch bei der Altersbestimmung nicht ohne die Mathematik aus. Aber keine Sorge, nur Grundkenntnisse in Bezug auf Exponentialfunktionen sind nötig.
Bei der Bestimmung einer Gleichung für den radioaktiven Zerfall, haben wir uns an einem Graphen, der den radioaktiven Zerfall beschreibt, orientiert.
| Im nebenstehenden Graphen ist die Aktivität einer Probe in Abhängigkeit von der Zeit wiederge- geben. |
 |
Anhand der Form dieses Graphen kann man vermuten, dass es sich um eine Exponentialfunktion mit negativem Exponenten handelt. Eine allgemeine Form dieser Funktion ist:
Zur genaueren Bestimmung der Gleichung müssen für a und k genauere Angaben gemacht werden. Da a den Wert angibt, bei dem der Graph die y-Achse schneidet, muss hier der Funktionswert zu Anfang des Zerfalls gewählt werden. Der Faktor k im Exponent gibt die Größe des Zerfalls an, somit die Zerfallskonstante (l) des zerfallenden Stoffes. Da die Funktion bestimmten Zeitpunkten Funktionswerte zuordnet, ist für x hier t zu wählen. Der Faktor 1 im Exponenten wurde aus den genannten Gründen gewählt, weil der Graph eine Exponentialfunktion darstellt, die an der y-Achse gespiegelt ist. Daraus leitet man folgende Beziehungen ab:
; mit N0: Anzahl der Teilchen zu Anfang des Zerfalls
Analog gilt dies auch für die Aktivität, da sie proportional zur Anzahl der radioaktiven Teilchen ist:
; mit A0: Aktivität zu Anfang des Zerfalls
Die Halbwertszeit gibt die Zeitspanne t an, in der die Hälfte der vorhandenen Teilchen zerfallen ist, oder nach der nur noch die Hälfte der Ausgangsaktivität vorhanden ist. Wenn eine Halbwertszeit berechnet werden soll, führt man folgende Umformungen durch:
Ausgangsgleichung war: 
Wird die Halbwertszeit th genannt, folgt:
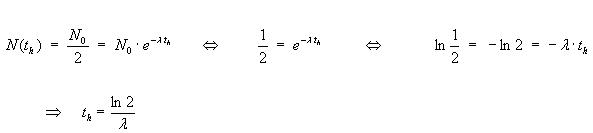
Da häufig keine Angaben über die spezifische Zerfallskonstante λ gemacht werden, sondern nur über die Halbwertszeit des zerfallenden Stoffes, ist es sinnvoll die Zerfallsgleichung bezüglich dieser umzuformen:
Aus:
folgt: |
 |
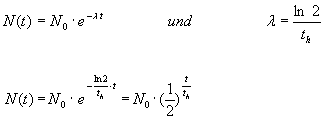Möchte man ermitteln, wie viele Teilchen in einem bestimmten Zeitraum ∆t zerfallen sind, so gibt es hierfür zwei verschiedene mathematische Formeln. Zu beachten ist bei beiden, dass das Ergebnis ∆N bei einer positiven Zeitspanne ∆t negativ ist, da die Anzahl der vorhandenen Teilchen ja immer geringer wird. Die erste Möglichkeit ist:
Für kleine Werte ∆t ist oft folgende Abschätzung sinnvoll:
wird abgeleitet nach der Zeit (dargestellt durch einen Punkt über dem N)
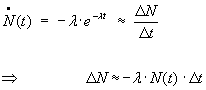
Als am 19.09.1991 das Ehepaar Erika und Helmut Simon bei einer Wanderung auf dem Schnalstaler Gletscher eine Leiche fand, war ihnen die Tragweite ihrer Entdeckung noch gar nicht bewusst. Nach wissenschaftlichen Untersuchungen fand man heraus, dass der Leichnam dort 5200 Jahre ungestört gelegen hatte. Der Fund erregte weltweit großes Aufsehen und wurde schlagartig berühmt. Man gab ihm den Namen Ötzi, unter dem er heute jedem bekannt ist.
Im folgenden werden die physikalischen Methoden dazu näher erläutert, die es möglich machten, Ötzis Alter so genau zu bestimmen. Aber keine Angst — Du musst kein Diplomphysiker dafür sein!
Bei der Altersbestimmung von Ötzi setzte man eine Methode ein, die sich die natürliche Radioaktivität zunutze macht. Mit dieser Methode ist es möglich alle organischen, kohlenstoffhaltigen Materialien in einem Zeitraum von 1.650 bis ungefähr 40.000 v.Chr. relativ exakt zu datieren. Sie wurde von dem amerikanischen Chemiker und Geophysiker Willard F. Libby entwickelt und steht seit 1946 der Wissenschaft zur Verfügung und hat die Bezeichnung Radiokarbon- oder Kohlenstoff-14-Methode.
Von unserer Sonne und anderen Sternen des Universums trifft ständig eine hochenergetische Strahlung auf die Atmosphäre der Erde. Diese kosmische Strahlung besteht zum großen Teil aus Protonen, 
- Teilchen, 
-Quanten und Elektronen, die unter der Primärstrahlung zusammengefasst sind. Diese Strahlung hat so hohe Energie, dass sie Stickstoff- und Sauerstoffatome beim Aufprall zerstören, sobald sie auf die obersten Schichten der Erdatmosphäre trifft. Bei einer Kollision entstehen Elementarteilchen, neue Atomkerne und Neutronen. Diese Neutronen wiederum erzeugen in einer Kettenreaktion weitere freie Neutronen, wenn sie auf Luftmoleküle treffen. Dies wird als Sekundärstrahlung bezeichnet.
In den Luftmolekülen befinden sich Kerne von Stickstoffatomen mit der Massezahl 14. Sie bestehen aus 7 Protonen und 7 Neutronen. Sobald ein freies Neutron auf den Kern trifft, wird ein Proton abgestoßen und das freie Neutron stattdessen aufgenommen. Der Kern hat seine Zusammensetzung aus Neutronen und Protonen geändert, während die Masse gleich blieb. Daraus entstand ein neuer Stoff und aus dem Stickstoffatom 
bildete sich das radioaktive Kohlenstoffisotop 
.
Das Verhältnis zwischen 
und dem stabilen 
, das ca. 99% des gesamten Kohlenstoffvorkommens ausmacht, kann für den Zeitraum der ganzen Menschheitsgeschichte als konstant angesehen werden.
In der Erdatmosphäre kommt Kohlenstoff meist in der Verbindung 
, also Kohlenstoffdioxid vor. Dieses Kohlenstoffdioxid, und damit auch das 
, wird durch die Fotosynthese von Pflanzen aufgenommen und in deren Organismus eingebaut. Über die Nahrungskette gelangt dann 
in die Körper von Tieren und schließlich auch in den von Menschen. Durch Ausatmen und andere Körperausscheidungen wird 
wieder abgegeben, sodass sich ein Gleichgewicht zwischen 
-Aufnahme und -Abgabe im Körper einstellt. Darum bleibt der 
-Gehalt im Körper des Menschen weitgehend konstant. Das ist nicht nur heute so. Die gleichen Bedingungen galten für die Zeit, in der Ötzi noch lebte.
Sobald ein Organismus stirbt, steht er nicht mehr im Austausch mit seiner Umwelt. Folglich kann ein toter Organismus auch kein 
mehr aufnehmen. Als Ötzi starb, konnte sein Körper also weder weiteres 
aufnehmen noch abgeben. Doch der 
-Gehalt bleibt über Tausende von Jahren nicht gleich. Weil es sich bei 
um ein radioaktives Isotop handelt, ist es nicht stabil und zerfällt mit der Zeit zu seinem Ausgangselement Stickstoff. Dabei verringert sich die Radioaktivität alle 5.730 Jahre auf die Hälfte.
Mit entsprechenden Messgeräten (Geiger-Müller-Zählrohr, Massenspektrometer) konnte man die verbliebene Radioaktivität von Ötzis konserviertem Gewebe messen. Diese Messungen ergaben, dass bei unserem Ötzi nur noch 53 % der Zerfälle von Kohlenstoff-14-Atomen stattfindet. Mithilfe der Zerfallsgleichung lässt sich folgende Gleichung aufstellen:
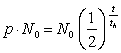
wobei p der Prozentsatz ist, der die verbliebenden C14-Atome angibt, th steht für die Halbwertszeit, in unserem Fall also 5.730 Jahre.
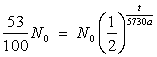
t gibt die Zeit an, die verstreichen muss, damit so viele C14-Atome zerfallen können. Um also das Alter zu bestimmen, muss man die Gleichung nach t umstellen:
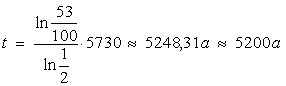
Dieses Vorgehen ist allerdings nicht perfekt. Die Sonnenaktivität hat sich im Laufe der Geschichte verändert, wodurch der C14-Gehalt der Atmosphäre variierte. Diese Tatsache muss man bei den Rechnungen beachten, etwa durch eine entsprechende Eichkurve. Durch das Bestimmen des Alters von unterschiedlich alten Holzproben, deren Alter allerdings schon vorher bekannt war, konnte man eine solche Eichkurve erstellen.
Außerdem lässt sich diese Methode nicht auf sehr kleine Proben anwenden, da man aufgrund seiner geringen Radioaktivität mindestens einige Gramm von Kohlenstoff-14 benötigt, um den Prozentsatz p genau zu bestimmen.
Da wir nun wissen, wie alt Ötzi ist, ist es nun auch von Interesse, zu erfahren, wie alt die Erde ist. Dazu gibt es verschiedene Ansätze, z.B. die Bibel, die Rubidium-Strontium-Methode oder die Uran-Blei Methode, mit der wir uns hier näher befassen.
Dafür benutzen wir zuerst einmal die Steine, da diese wahrscheinlich die ältesten Dinge auf der Erde sind. Das Alter der Steine können wir abschätzen, da es die natürlichen Zerfallsreihen gibt. Manche Gesteinsarten enthalten seit dem Zeitpunkt ihrer Entstehung einen kleinen Anteil Uran 238U. Ein Teil dieses Urans ist bis heute (mit einer Halbwertszeit von 4,5 Milliarden Jahren) zu Blei 206Pb zerfallen.
Nehmen wir zunächst an, dass das gesamte Blei 206Pb in der Gesteinsprobe aus 238U entstanden ist. Dann ist das Verhältnis der Bleimenge zur Uranmenge ein Maß für das Alter des Gesteins. Je älter das Gestein, umso größer ist inzwischen der Bleianteil. Die genauere Erläuterung dieses Verhältnisses kann man unten nachlesen. Allerdings basiert die Rechnung auf einer unsicheren Annahme. Es ist nicht auszuschließen, dass ein Teil des Bleis 206Pb von vornherein in der Probe enthalten war und nicht durch Uranzerfall entstanden ist. Um diese Unsicherheit aus dem Weg zu räumen, vergleicht man die vier stabilen Bleiisotope in nicht uranhaltigen Gesteinen miteinander. Für unsere Betrachtung wichtig ist z.B., dass sie ca. 17 mal so viele 206Pb-Atome wie 205Pb-Atome enthalten. Letzteres kommt in den natürlichen Zerfallsreihen nicht vor, es kann also nicht durch Uranzerfall entstanden sein. Durch Ermittlung des 206Pb-Gehalts kann man (aufgrund des konstanten Verhältnisses der Mengen der natürlichen Bleiisotope) abschätzen, wie viel Blei 206Pb von vornherein in der Probe war, der Rest ist wahrscheinlich durch Uranzerfall entstanden.
Für Meteoriten ergibt die Uran-Blei-Methode ein Alter von 4,5 Milliarden Jahren. Meteoriten sind damit ebenso alt wie die ältesten Mond- und Marsproben.
Die ältesten Erdgesteine sind 3,6 Milliarden Jahre alt. Wahrscheinlich ist die Erde gleichzeitig mit den übrigen Planeten des Sonnensystems entstanden. Durch Plattentektonik und Vulkanismus wurde die Erdkruste aber wieder aufgeschmolzen, dabei haben sich die ältesten Uranerze mit anderen Gesteinen gemischt und aufgelöst.
Zu dieser Datierungsmethode gibt es, wie zu fast allen, viele wissenschaftliche, aber vor allem pseudowissenschaftliche Informationen.
Die einzelnen Schritte der Altersbestimmung werden in folgender Übersicht mit Rechenweg dargestellt. Anhand der Tabelle lässt sich das Verfahren der Uran-Blei-Methode schrittweise durchführen.
Weitere Beispiele und Aufgaben zu dieser Methode folgen im Kapitel Anwendungen.
|
Beschreibung |
Rechnung |
|
| A | Anzahl der Atome in der Mineralprobe bestimmen | |
| Sind wie in den meisten Fällen nur Massenangaben für die Mineralienprobe angegeben muss die Anzahl der Atome jeweils errechnet werden. | ||
| 1 | Angaben in kg umrechnen. | Angaben erfolgen hier oft in mg. |
| 2 | Für die Anzahl N der Atome eines Elements ergibt sich mit der Masse m und Massenzahl z: |
wobei für u gilt:  |
| B | Blei206-Gehalt der Probe ermitteln | |
Befindet sich  in der Probe, kann der Anteil des durch Uranzerfall entstanden  bestimmt werden. |
||
| 1 |  ist die Anzahl aller Atome  -Atome;
 ist die Anzahl aller durch Uranzerfall entstandenen Blei-Atome. |
|
|
C |
Altersbestimmung |
|
 wird mit Pb,  mit U abgekürzt. (Index 0: Entstehung/ Index 1: Heute) |
||
| 1 | Aus U-Atomen sind Pb-Atome entstanden. Somit ist die Gesamtanzahl letztlich unverändert geblieben. |  |
| 2 | Die aktuelle Anzahl der Blei-Atome lässt sich als Vielfaches der Uran-Atome schreiben. Beide Werte sind bekannt. |
 |
| 3 | Ergebnis aus 2 in 1 einsetzen. |  |
| 4 | In Zerfallsgleichung lässt sich einsetzen und umformen. t ist das gesuchte Alter. (N jeweils die Anzahl der Atome von Uran)  |
  einsetzen:  |
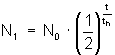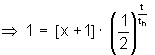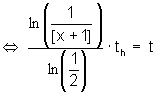1)
In einer Höhle wurden Reste an Holzkohle gefunden, die aufgrund ihres Gehaltes an 
nur noch eine Aktivität von 
aufwiesen.
Wie alt ist die Holzkohle?
2)
1g Kohlenstoff (aus einem antiken Schuh hergestellt) hatten 30% der Aktivität von 1g Kohlenstoff aus frischem Holz.
Berechne das Alter des Schuhs!
3)
An einer Mumie wurden 56,2% der Aktivität von 
gegenüber der in einer lebenden Substanz gemessen.
Wie alt ist die Mumie?
1)
Die chemische Untersuchung einer Gesteinsprobe ergab das folgende Massenverhältnis von 
zu 
: 0,2.
Berechne daraus das Alter der Gesteinsprobe!
2)
In einem uranhaltigen Mineral wurden 6 mg Uran und 0,9 mg Blei gefunden.
Wie alt ist das Mineral?
Zur Kohlenstoff-14 Methode:
1)
Aktuelle Aktivität: 
ursprüngliche Aktivität:
Daraus ergibt sich das Verhältnis von aktueller Teilchenzahl der 
Atome 
zu der ursprünglichen Teilchenzahl der 
Atome 
.
Nach dem Zerfallsgesetz mit der Halbwertszeit 
gilt:
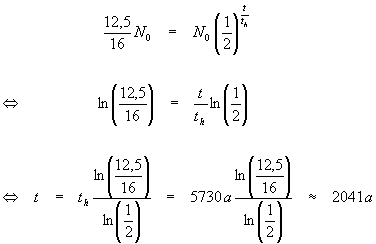
Die Holzkohle ist also ca. 2041 Jahre alt.
2)
Da das Verhältnis der aktuellen Aktivität zur ursprnglichen Aktivität 30% beträgt folgt für die aktuelle Teilchenzahl 
und die ursprüngliche Teilchenzahl 
:
Aus der Zerfallsgleichung folgt:
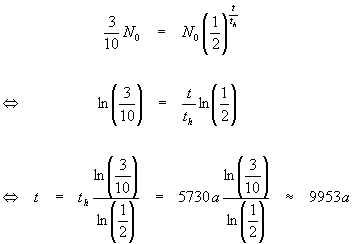
Das heißt der Schuh ist ungefähr 9953 Jahre alt.
3)
Aus dem Verhältnis von aktueller Aktivität zur ursprünglichen Aktivität 56,2% folgt das Verhätnis von aktueller Teilchenzahl 
zur ursprünglichen Teilchenzahl 
:
Aus der Zerfallsgleichung folgt:
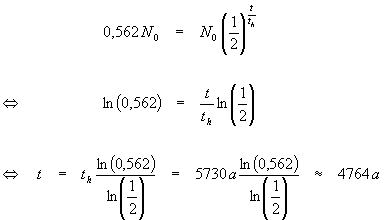
Also ist die Mumie ca. 4764 Jahre alt.
Zur Uran-Blei Methode:
1)
Aus dem gegebenen Massenverhältnis der Masse von 
zur Masse von 
folgt mit der atomaren Masseneinheit u und den aktuellen Teilchenzahlen für Blei und Uran:
Das heißt bis heute sind 
Atome zerfallen. Nicht zerfallen sind 
Atome. Bei der Entstehung des Gesteins, also zum Zeitpunkt an dem noch kein Uranatom zerfallen ist, betrug die Teilchenzahl des Urans demnach 
.
Aus dem Zerfallsgesetz folgt mit der Halbwertszeit von Uran 
:
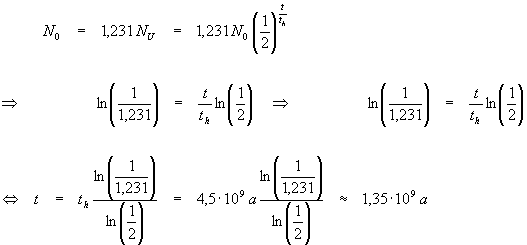
Die Gesteinsprobe ist ungefähr 
Jahre alt.
2)
Das Massenverhältnis beträgt:
für das Verhältnis der aktuellen Teilchenzahlen gilt:
Bis heute sind also 
Atome zerfallen. Nicht zerfallen sind 
Atome. Bei der Entstehung des Minerals, betrug die Teilchenzahl des Urans demnach 
.
Aus dem Zerfallsgesetz folgt mit der Halbwertszeit 
:
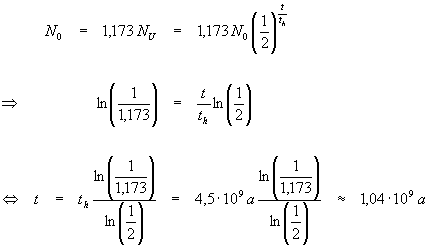
Also ist das Mineral ca. 
Jahre alt.
Zum Download dieses Dokuments einfach auf das gewünsche Format klicken
Als Adobe Portable Document File (.pdf)
Als Microsoft Word Dokument (.doc)
Dieses HTML-File mit allen Bildern gepackt in einem ZIP-Archiv (.zip)
Bearbeitung des HTML-Codes: Guido Freitag